HyperFedX: Explainable Federated Learning with Free-Rider Prevention
 HyperFedX Framework
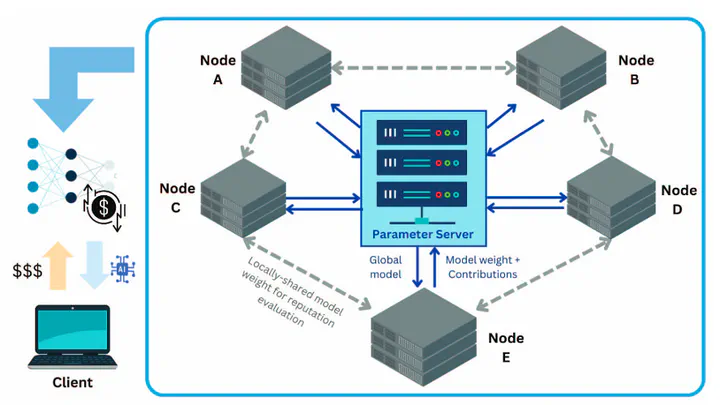
HyperFedX Framework
Core Discovery
We developed HyperFedX, a framework that uses hypernetworks and gradient explainers to detect free-riders in federated learning systems, providing transparency while improving distributed model training reliability.
Why It Matters
This research addresses a critical vulnerability in federated learning systems. Free-riders undermine collaborative learning by contributing random or untrained weights while benefiting from the global model. HyperFedX not only detects these participants but establishes a transparent evaluation mechanism that maintains system integrity and fairness.
Key Innovations
- Hypernetwork Architecture: Dynamic weight allocation system adjusts contribution influence based on quality
- GradientExplainer Integration: Provides transparency into how participant contributions are evaluated
- Reputation-Based Incentives: Calculated from SHAP values to reward genuine contributors
- Adaptive Aggregation: Parameter server optimizes model updates for greater resilience
My Contributions
- Designed the hypernetwork-based adaptive aggregation algorithm
- Implemented the code to actualize the theoretical model
- Developed the utility-based decision modeling for free-rider detection
- Integrated GradientExplainer with the hypernetwork for transparent evaluation
- Created the SHAP-based incentive calculation framework
Go Deeper
Technical Approach
Our framework uses three key mathematical models to address free-rider detection and prevention:
1. Utility-Based Decision Model
$$U_i = P_i(Contribute) \times R_i(Contribute) - C_i(Contribute) - P_i(Free\text{-}Ride) \times P_i(Detection) \times F_i$$This model captures the decision-making process of participating nodes:
- $U_i$ represents the utility (benefit) a node receives
- $P_i(Contribute)$ is the probability of node i choosing to contribute
- $R_i(Contribute)$ is the reward for contributing
- $C_i(Contribute)$ is the cost of contributing (computational resources, etc.)
- $P_i(Free\text{-}Ride)$ is the probability of choosing to free-ride
- $P_i(Detection)$ is the probability of being detected as a free-rider
- $F_i$ is the penalty for being detected
This formulation allows us to model when nodes will rationally choose to free-ride versus contribute honestly. A node will contribute when $U_i > 0$ and free-ride when $U_i < 0$.
2. Incentive Calculation System
$$I_i = \frac{[\alpha \cdot Contribute_i + \beta \cdot Repute_i]}{\alpha + \beta} \times Profit$$Where:
- $I_i$ is the incentive allocated to participant i
- $Contribute_i$ measures the quality of current contribution based on: $$Contribute_i = \frac{(\sum_{j=1}^{C} dist_{i,j} \times SHAP_{i,j}) \times (\sum_{j=1}^{C} acc_{i,j} \times SHAP_{i,j+C})}{C}$$
- $Repute_i$ represents accumulated reputation from previous rounds: $$Repute_i = \frac{(\sum_{j=1}^{C} r \times SHAP_{i,j+2C})}{C}$$
- $\alpha$ and $β$ are weighting parameters that balance immediate contribution versus historical reputation
- $Profit$ is the total reward available for distribution
This system uses SHAP values to quantify the importance of each participant’s contribution in terms of both accuracy and distance from the global model, creating a transparent incentive mechanism.
3. Parameter Server Optimization
$$\min_{\theta,I_i,\forall i} L(\theta) \cdot [(-\sum_{i=1}^{E} U_i(I_i, \theta_i))/E]$$The parameter server objective function:
- Minimizes the model loss function $L(\theta)$ while simultaneously
- Maximizing the average utility $U_i$ across all participants
- $\theta$ represents the model parameters
- $I_i$ represents the incentives allocated to each participant
- $E$ is the total number of participants
This dual objective ensures the global model maintains high performance while creating conditions that encourage honest participation.
Implementation Architecture
The HyperFedX framework implementation consists of several key components:
-
Hypernetwork Component: We implemented a hypernetwork that takes four key inputs:
- Distance metrics measuring how far a participant’s model is from others
- Accuracy metrics of each participant’s model on validation data
- Reputation scores from previous rounds
- Current model parameters
-
GradientExplainer Integration: We applied SHAP values to interpret the hypernetwork’s decisions by:
- Computing gradients at multiple reference points
- Clustering gradients based on importance using K-means
- Selecting the most informative gradients to explain model decisions
-
Simulation Environment: We tested our framework against:
- Various free-rider scenarios (random weights, copied weights, etc.)
- Different network topologies and participant behaviors
- Multiple communication patterns and incentive structures
Research Connection
This work connects to advanced research in:
- Federated learning frameworks for edge computing
- Explainable AI applications in distributed systems
- Edge-LLM solutions for resource-constrained environments
Acknowledgments
Research conducted with the Intelligent Edge/Fog Computing Alliance Lab at NYCU, under Prof. Ching-Yao Huang’s guidance, with contributions from Sirapop Nuannimnoi and team members.